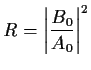|
|
Simulation of the Reflectivity 
A suitable theoretical method to describe the reflectivity and within the
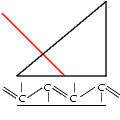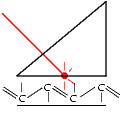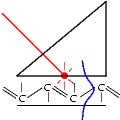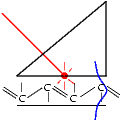
leaky modes of a thin layer or a multilayer system (see Figure below) is a matrix formalism after
Yeh ["Optical Waves in layered media",John Wiley and Sons 1988]. The electromagnetic wave is decomposed into a left and a right propagating component.
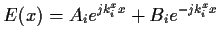 |
(1) |
The relation between the different Amplitudes 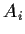 and and 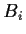 is given by a
matrix multiplication over all is given by a
matrix multiplication over all 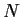 layers. layers.
![$\displaystyle \begin{pmatrix}A_0 \\ B_0 \end{pmatrix} = \frac{1}{t_{01}} \begin...
...{P_i} \right] \begin{pmatrix}A_{N+1}^{\prime} \\ B_{N+1}^{\prime} \end{pmatrix}$](rsimtheory/img6.gif) |
(2) |
Figure:
Nomenclature of a multilayer system
|
![\includegraphics [width=\textwidth]{figures/multilayersystem.eps}](rsimtheory/img7.gif)
|
From which the reflected intensity
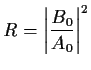 |
(3) |
can be calulated. The elements of the so called transfer Matrix 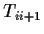 are
the fresnel coefficients for transmission and reflection at the interface
between two different media. The optical phase difference are
the fresnel coefficients for transmission and reflection at the interface
between two different media. The optical phase difference
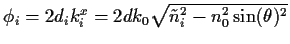 is
introduced by a phase matrix is
introduced by a phase matrix 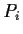 . The complex refractive index leads to a
real exponentional factor in the elements of the phase matrix which influences
strongly the intensity of the reflected light. . The complex refractive index leads to a
real exponentional factor in the elements of the phase matrix which influences
strongly the intensity of the reflected light.
This matrix calculation is a very general tool and it can easily be implemented on a computer calculating a large number (practically continuous) of layers N, simulating static or dynamic refractive index profiles.
|
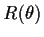
![$\displaystyle \begin{pmatrix}A_0 \\ B_0 \end{pmatrix} = \frac{1}{t_{01}} \begin...
...{P_i} \right] \begin{pmatrix}A_{N+1}^{\prime} \\ B_{N+1}^{\prime} \end{pmatrix}$](rsimtheory/img6.gif)
![\includegraphics [width=\textwidth]{figures/multilayersystem.eps}](rsimtheory/img7.gif)